論理思考学習コンテンツ
ロジックツリー

論理思考力×算数・数学で「未知の問題や難問」を
自力で突破できる学習指導コンテンツ!
■ 対象:小学4年生〜高校3年生
LOGICTREEプログラムの特長
社会生活や運動に体力が必要であるように、思考を続けるには「思考の体力」が必要です。LOGICTREEプログラムは、数学的思考力を身につけることで「思考の体力」を鍛える新しいプログラムです。「思考の体力」を育てるために段階的に目標を設定したステージを用意しており、それを自分自身の力で解決していくことで思考を深めていきます。
例えば東大
例えば、東大は難問は出しますが、決して奇問は出しません。頻出問題の解法を身につけ、良質の難問をじっくり考えて解く訓練を重ねれば合格につながります。そのために必要なのは「思考の体力」を身につけておくことです。
才能ではなく習慣(週1回50分)
今の教室に通う時間に、もうプラス50分。しっかりと考えるLOGICTREEプログラムの時間が、受講生の論理思考を育み、潜在能力を大きく育てます。
LOGICTREE プログラムの目標
1
数学の美しさ、考えることの楽しさを自分自身で体験していただきます。
2
難問にも十分に時間をかけて取り組めるような根気と好奇心を養います。
◆小学生から大学受験までの90段階編成
驚異の合格実績
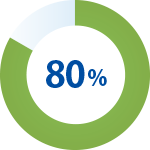
卒業生の半数は旧帝大または国立医学科に進学。8割の生徒が国公立大学に進学。
旧7帝国大学
東京大学・京都大学・大阪大学・東北大学・名古屋大学・九州大学・北海道大学
国立大学医学部医学科
東京大学理科Ⅲ類・京都大学医学部・大阪大学医学部・東北大学医学部・名古屋大学医学部・九州大学医学部・神戸大学医学部
【東京大学 理科Ⅲ類合格】岡田 展幸さん(2017国際数学オリンピック銅メダル 受賞)
◆ライバルとの差を決定づけるのは、答えを導き出す過程にある
数学というとまず1番に、詰め込み式を想像する方が多いかと思います。まず公式を覚えて、次に明らかに公式を使えば一発で解ける問題が並べられています。入試を意識したテキストなら、それに加えて発展問題が2〜3問あるという感じでしょうか。私もそれが一般的で、詰め込み式の数学しかできないとばかり思っていました。でも違いました。LOGICTREEのテキストでは、単に公式の練習ではない、よく練られた良問が並びます。解けたときの喜びはやってみないとわからないし、途方もない所から答えを導いて行く力はライバルとの差を決定づけるものとなります。
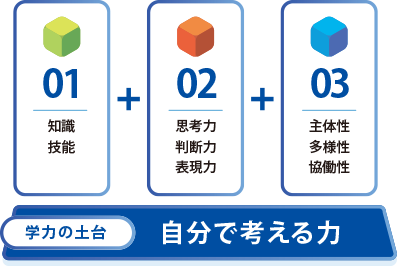
近年の入試改革や学習指導要領改定に伴って、受験で求められる能力が大きく変わり、「知識・技能」に加えて「思考力・判断力・表現力」を評価するための試験へと移行しました。「まねる」学習よりも、自分で「考える力」が必要となっていきます。
◆生徒のやる気を継続させる認定証
「数量」「図形」「思考」「論理」の4つの分野を中心に、試行錯誤して思考の型を身につけることを目的としています。数を量として認識する力・図形認識力、「無から有を創造すること」ができる、レベルの高い論理思考力を育成します。未知のものに対してしっかりと取り組み、自分で考えて解決していくことで、学習の本来の楽しさを実感し、ステップごとにもらえる認定証と合わせてやる気を継続させることができます。
◆自分自身で解決していくことで力がついていく仕組み


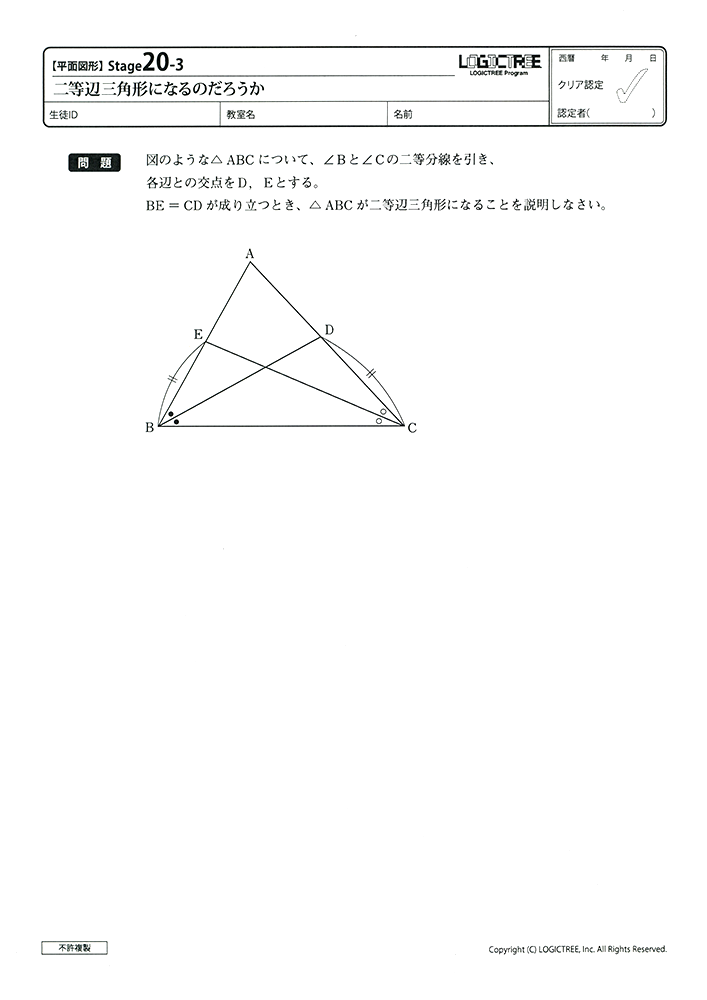
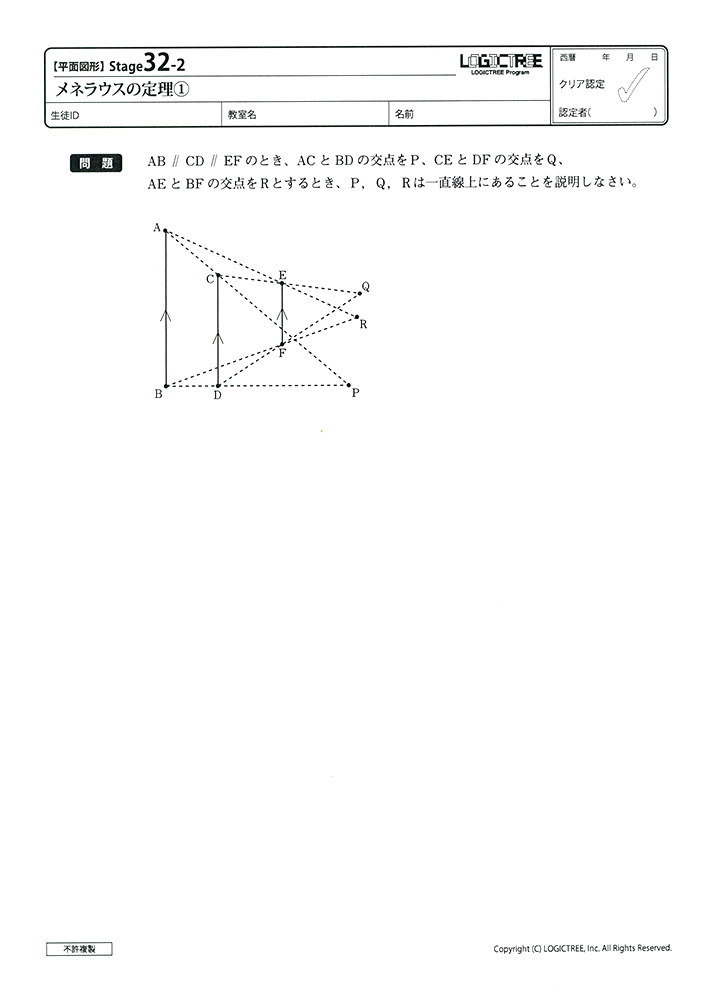



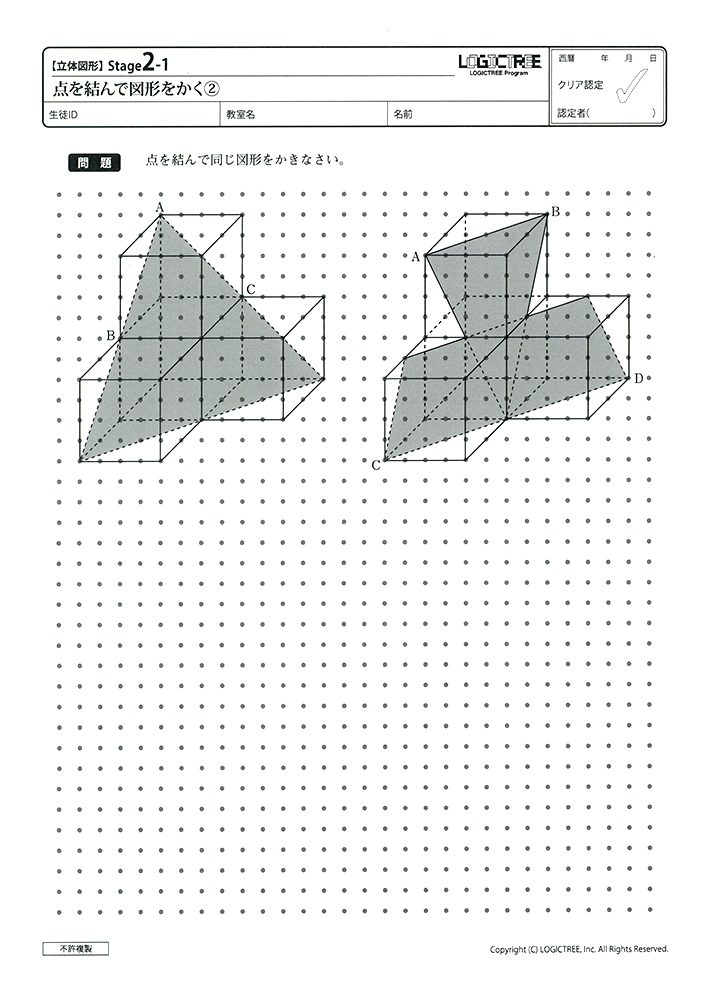
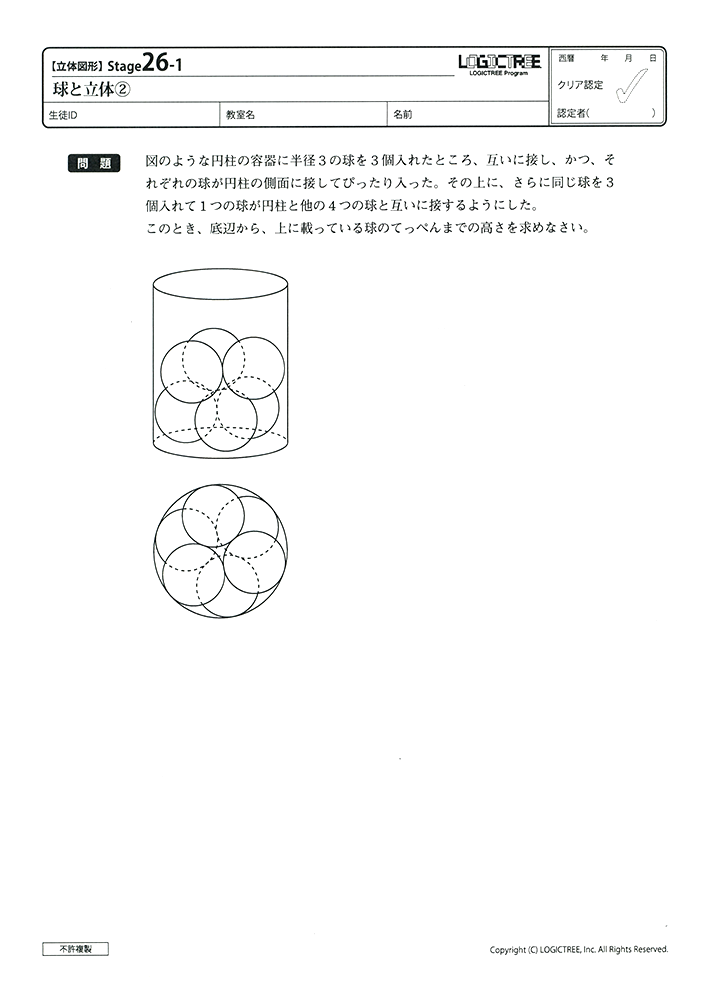
【レギュラーコース教材見本】
中学生以上を対象とした難しいコース


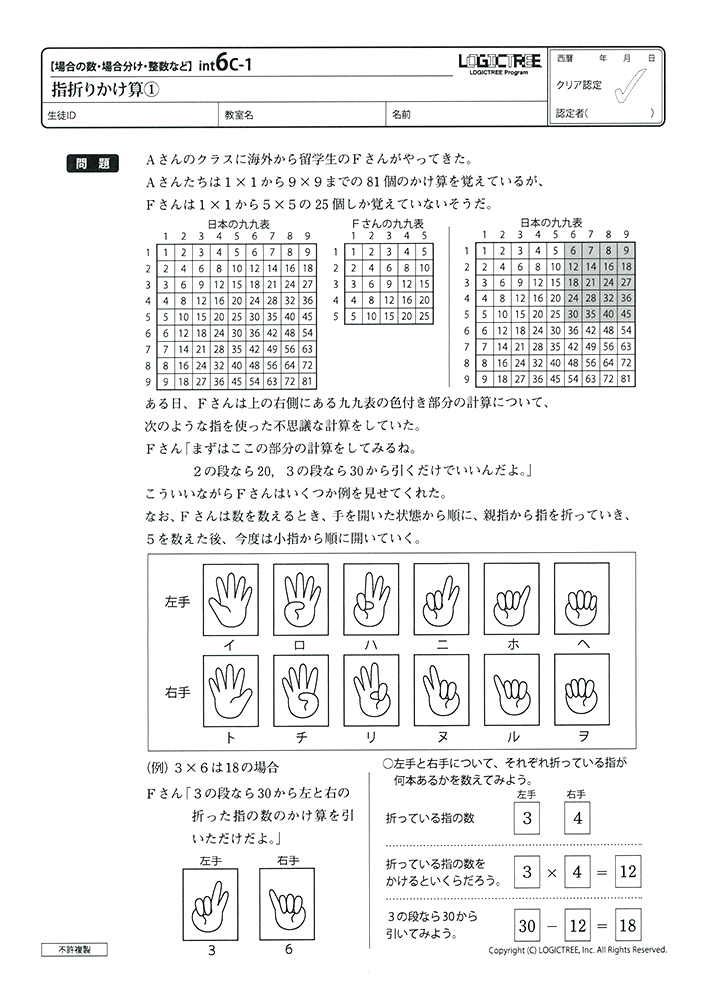
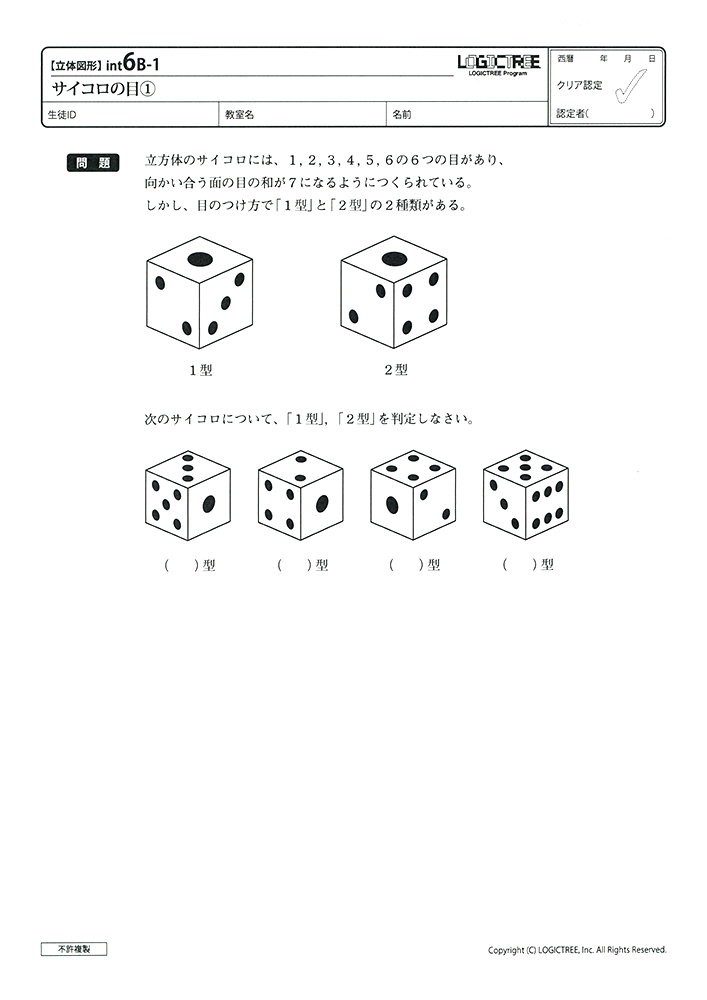
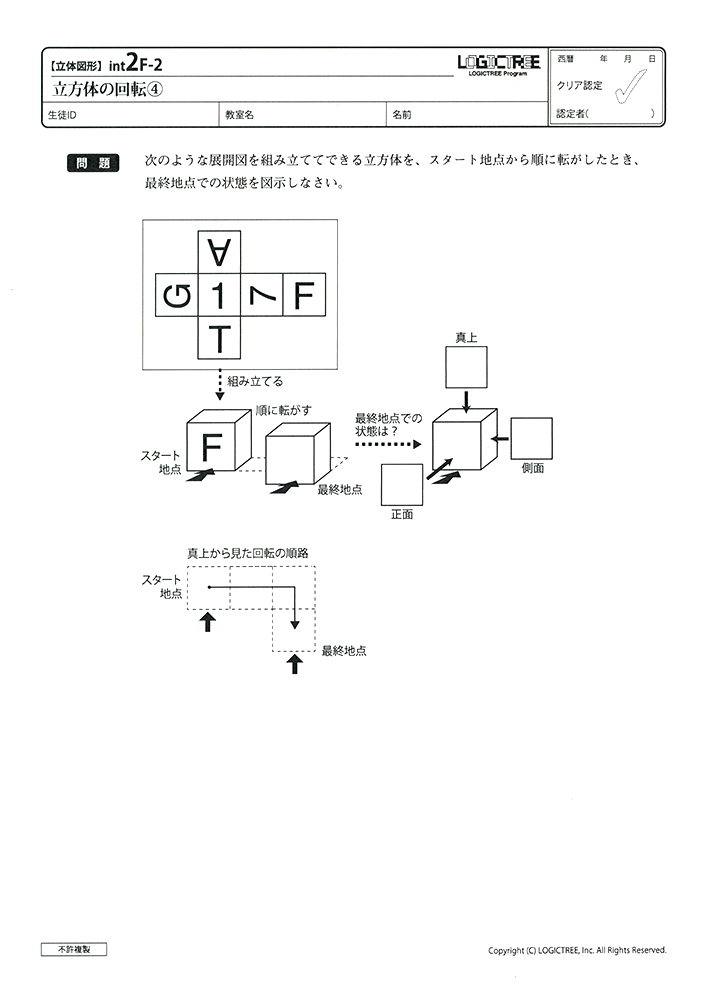


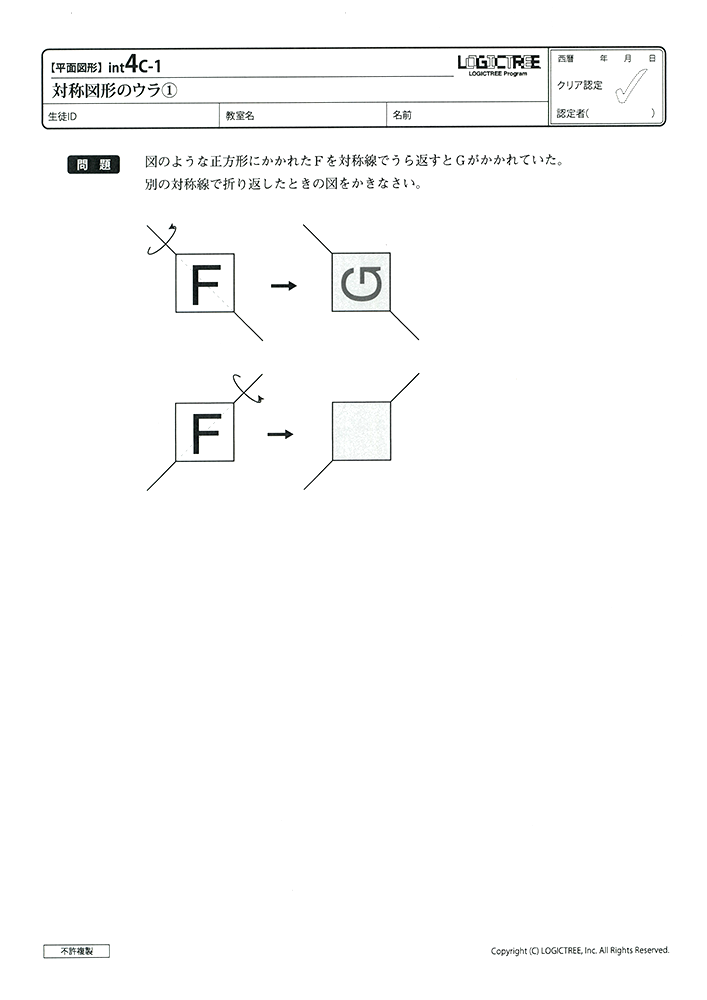
【インテンシィブコース教材見本】
小学生から使える入門コース
問題の一例
和(はかり)の使い方
問題の一例
ナンバーロジック
0から9の数字が書いてあるカードが、それぞれ1枚ずつある。この中から数字「1」のカードを選び、数字の前に「−(マイナス) 」の記号をつける。更に3枚を選び、数字の前に「−(マイナス)」 の記号をつけると、すべてのカードの合計は3になった。その後、このカードをA,B,Cの3つのグループに分けると、グループ Aは4枚のカードの積が864、グループBの4枚のカードの和が 1、グループCは2枚のカードの積が0となった。各グループに属する数を求めなさい。

問題の一例
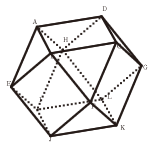
切り口を考える
1辺の長さが6cmである正方形6面と、正3角形8面で立体をつくると、右図になる。辺BEの中点を通り、面ABCDと平行に切ったときの切り口の面積を求めなさい。
問題の一例
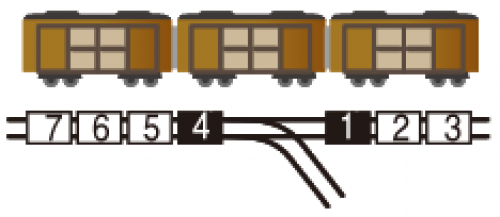
貨物列車の動き
3両編成と4両編成の2つの貨物列車が次のように並んでいる。各先頭車両の[1]と[4]は前にも後ろにも進むことができる。 また、[2]、[3]、[5]、[6]、[7]は貨物車両で[1]または[4]と連結していかなければ動くことはできない。また、側線は、車両1両しか入らない長さである。貨物列車がうまくすれ違う方法を答えなさい。